Управление по делам образования г.Челябинска

Учебно-методический центр г.Челябинска

Служба информационно-аналитического обеспечения Калининского района г.Челябинска

Олимпийский образовательный портал

Вход в Электронный журнал

Блог АС "Сетевой город.Образование"

Информация и знания. Человек получает информацию из окружающего мира с помощью органов чувств, анализирует ее и выявляет существенные закономерности с помощью мышления, хранит полученную информацию в памяти. Процесс систематического научного познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и так далее). Таким образом, с точки зрения процесса познания информация может рассматриваться как знания.

Процесс познания можно наглядно изобразить в виде расширяющегося круга знания (такой способ придумали еще древние греки). Вне этого круга лежит область незнания, а окружность является границей между знанием и незнанием. Парадокс состоит в том, что чем большим объемом знаний обладает человек (чем шире круг знаний), тем больше он ощущает недостаток знаний (тем больше граница нашего незнания. мерой которого в этой модели является длина окружности) - рис. 1.

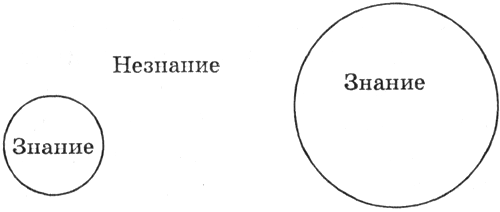
Рис. 1. Знание и незнание

Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию.

Например, после сдачи экзамена по информатике вы мучаетесь неопределенностью, вы не знаете какую оценку получили. Наконец, экзаменационная комиссия объявляет результаты экзамена, и вы получаете сообщение, которое приносит полную определенность, теперь вы знаете свою оценку. Происходит переход от незнания к полному знанию, значит, сообщение экзаменационной комиссии содержит информацию.

Уменьшение неопределенности знаний. Подход к информации как мере уменьшения неопределенности знаний позволяет количественно измерять информацию, что чрезвычайно валено для информатики. Рассмотрим вопрос об определении количества информации более подробно на конкретных примерах.

Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий - монета окажется в одном из двух положений: "орел" или "решка".

Можно говорить, что события равновероятны, если при возрастающем числе опытов количества выпадений "орла" и "решки" постепенно сближаются. Например, если мы бросим монету 10 раз, то "орел" может выпасть 7 раз, а решка - 3 раза, если бросим монету 100 раз, то "орел" может выпасть 60 раз, а "решка" - 40 раз, если бросим монету 1000 раз, то "орел" может выпасть 520 раз, а "решка" - 480 и так далее.

В итоге при очень большой серии опытов количества выпадений "орла" и "решки" практически сравняются.

Перед броском существует неопределенность наших знаний (возможны два события), и, как упадет монета, предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение), что монета в данный момент находится в определенном положении (например, "орел"). Это сообщение приводит к уменьшению неопределенности наших знаний в два раза, так как до броска мы имели два вероятных события, а после броска - только одно, то есть в два раза меньше (рис. 2).

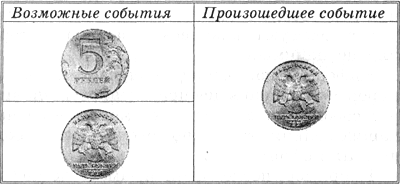
Рис. 2. Возможные и произошедшее события

Чем больше количество возможных событий, тем больше начальная неопределенность и соответственно тем большее количество информации будет содержать сообщение о результатах опыта.

Единицы измерения количества информации. Для количественного выражения любой величины необходимо определить единицу измерения. Так, для измерения длины в качестве единицы выбран метр, для измерения массы - килограмм и так далее. Аналогично, для определения количества информации необходимо ввести единицу измерения.

За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность в два раза. Такая единица названа "бит".

Если вернуться к опыту с бросанием монеты, то здесь неопределенность как раз уменьшается в два раза и, следовательно, полученное количество информации равно 1 биту.

Минимальной единицей измерения количества информации является бит, а следующей по величине единицей является байт, причем

1 байт = 23 бит = 8 бит

В информатике система образования кратных единиц измерения количества информации несколько отличается от принятых в большинстве наук. Традиционные метрические системы единиц, например Международная система единиц СИ, в качестве множителей кратных единиц используют коэффициент 10n, где п = 3, 6, 9 и так далее, что соответствует десятичным приставкам Кило (103), Мега (106), Гига (109) и так далее.

Компьютер оперирует числами не в десятичной, а в двоичной системе счисления, поэтому в кратных единицах измерения количества информации используется коэффициент 2n.

Так, кратные байту единицы измерения количества информации вводятся следующим образом:

1 Кбайт = 210 байт = 1024 байт;
1 Мбайт = 210 Кбайт = 1024 Кбайт;
1 Гбайт = 210 Мбайт = 1024 Мбайт.

Количество возможных событий и количество информации. Существует формула, которая связывает между собой количество возможных событий N и количество информации I:

По этой формуле можно легко определить количество возможных событий, если известно количество информации. Например, если мы получили 4 бита информации, то количество возможных событий составляло:

N = 24 = 16.

Наоборот, для определения количества информации, если известно количество событий, необходимо решить показательное уравнение относительно /. Например, в игре "Крестики-нолики" на поле 8x8 перед первым ходом существует 64 возможных события (64 различных варианта расположения "крестика"), тогда уравнение принимает вид:

64 = 2ⁱ.

Так как 64 = 26, то получим:

26 = 2ⁱ.

Таким образом, I = 6 битов, то есть количество информации, полученное вторым игроком после первого хода первого игрока, составляет 6 битов.